Tous les mouvements peuvent se décomposer en somme de deux mouvements élémentaires : la translation et la rotation.
La translation
On dit qu’un solide est en translation si tout segment de ce solide conserve sa direction lors du déplacement.
Si on trace la direction (= droite qui sert de support) d'un segment à différents instants, on obtient des droites paralèlles.
Remarque
Une translation peut se faire selon différentes trajectoire (trajectoire = trace laissée par un point dans un référentiel donné, nous reviendrons sur la notion de référentiel juste après...)
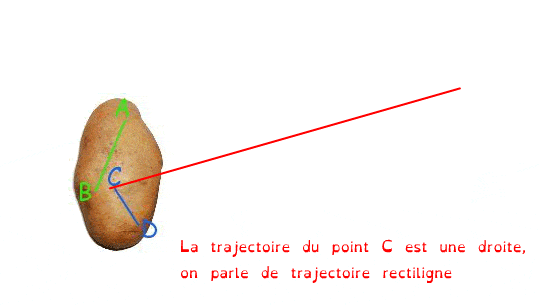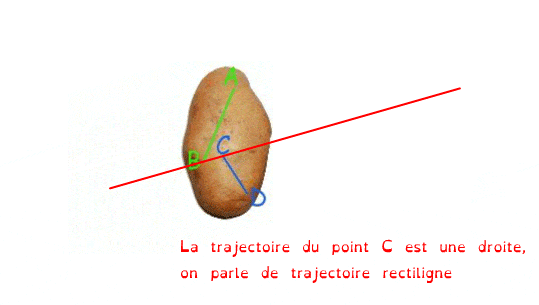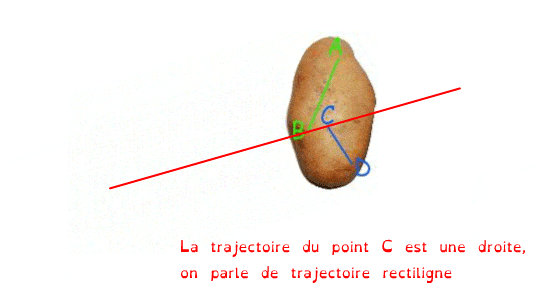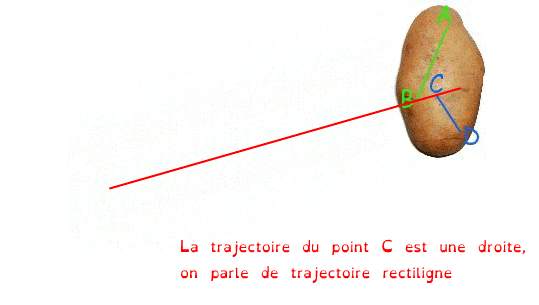
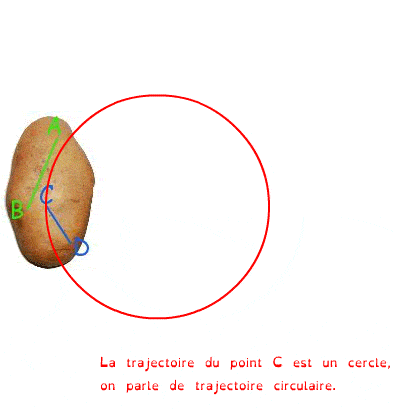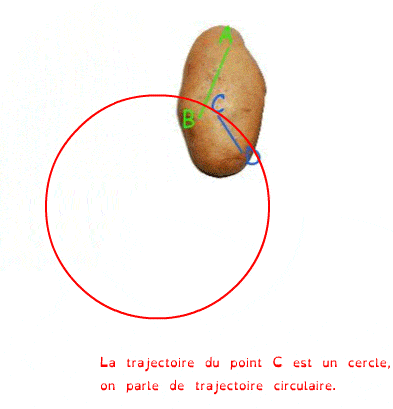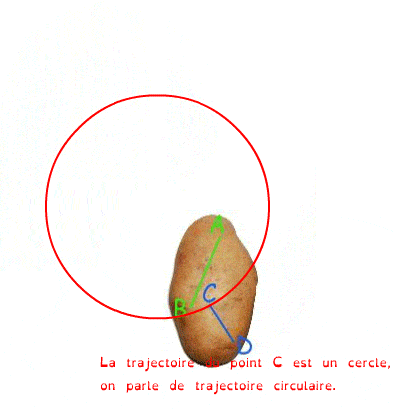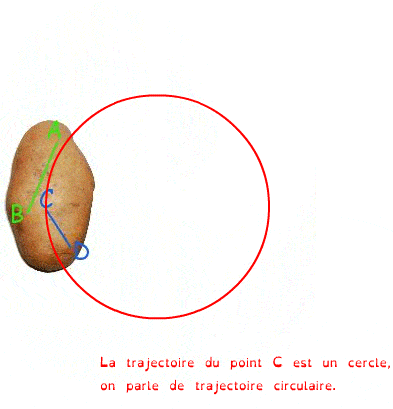
La rotation
On dit qu’un solide est en rotation si les trajectoires de tous ses points sont des cercles centrés sur le même axe.
Cet axe de rotation est perpendiculaire aux plans des cercles.
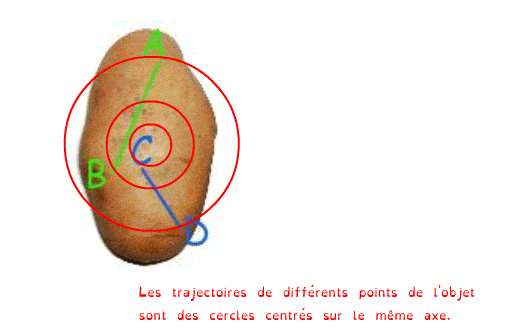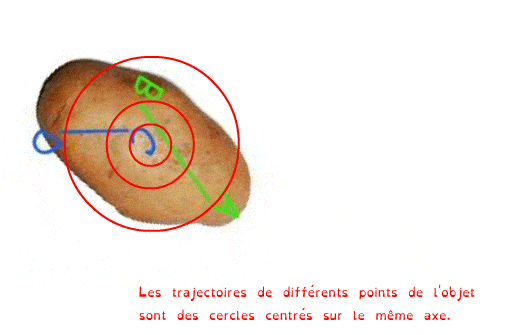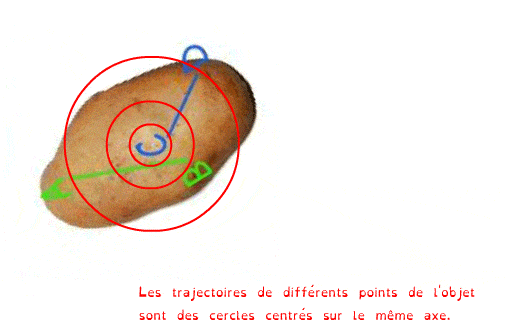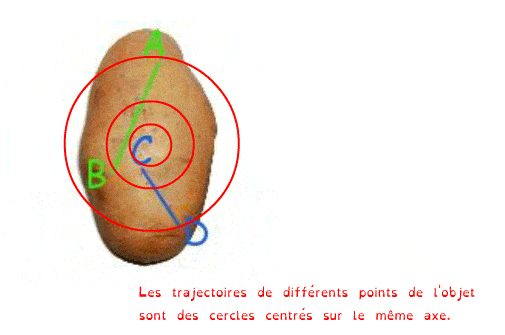
Et pourquoi des patates ? Eh bien parce que le "patatoïde" est utilisé en mécanique pour désigner un objet quelconque sans axe ni centre de symétrie afin de s'assurer qu'il n'y ai pas de rotation masquée entre deux positions de l'objet...
Voici un film publicitaire de la société FANUC qui construit les robots utilisés sur les chaines de fabrication de différentes marques automobiles (Audi dans cette vidéo). L'objet n'est pas, bien sûr, de faire de la publicité pour ces marques mais d'observer les mouvements des robots, rotations multiples pour articuler les bras agiles des robots et translation des carcasses des véhicules.
Relativité du mouvement : importance du référentiel
Lorsqu'on est assis dans un train (référentiel "lié" au train : dont l'origine est un point du train), le siège devant nous ne bouge pas. Mais pour le voyageur sur le quai d'une gare qui regarde passer le train (référentiel dit "terrestre", lié au sol), ce train et tout ce qu'il contient est en mouvement (y compris moi et le siège de devant...).
Un mouvement ne peut donc se définir qu'en fonction du référentiel choisit pour l'observer : le train n'est en mouvement que pour un observateur situé à l'extérieur du train. Ce référentiel fixe l'origine du repère (des axes gradués qui vont permettre de mesurer des positions par exemple) liée à la position de l'observateur.
en animation par JP Fournat (www.pccl.fr)
En vidéo par Yannick Sayer
Cette relativité du mouvement explique en partie la difficulté qu'a eu l'Homme pour passer du modèle géocentré (la Terre immobile autour de laquelle tourne le reste de l'Univers) d'Hipparque promu par Ptolémée (Ier siècle après JC) au modèle héliocentré (la Terre tourne autour du Soleil) de Copernic (XVIe siècle) : pour prendre conscience du mouvement terrestre, il est difficile de se placer "à l'extérieur" de notre planète !